こんにちは!
みなさんは受験業界や浪人界隈に入り浸ったことはあるでしょうか?
そこではよく
二浪は現役だからセーフ
という言葉が飛び交っています。
これは本当なのでしょうか?
今回はこれの真偽を数学的帰納法を用いて証明したいと思います。
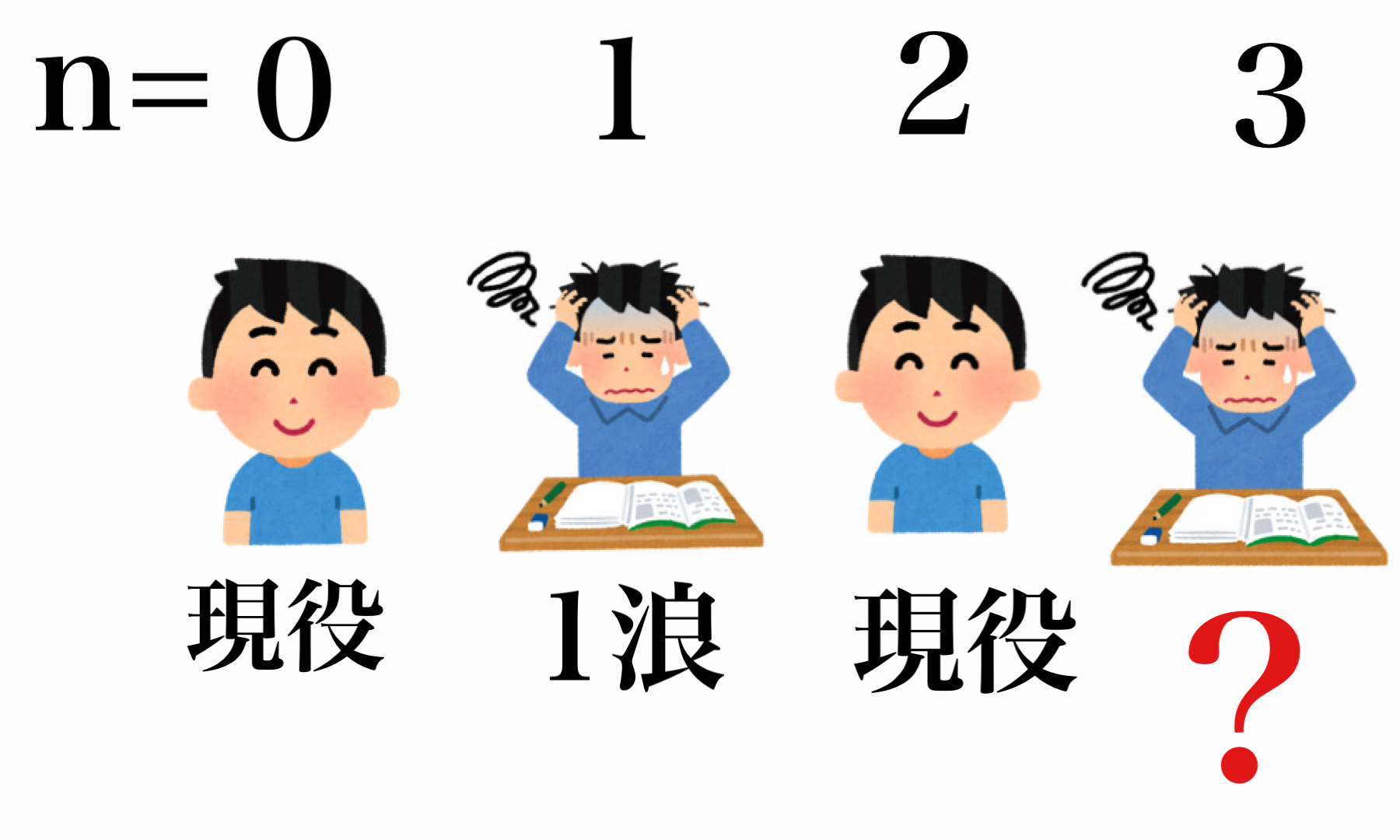
よく自分の浪人した回数をn=x(一浪ならn=1)のように表すので、今回もそのように表記します。
※ネタ記事です、マジレスはご勘弁ください
二浪が現役なわけないです
数学的帰納法を用いた『二浪は現役』であることの証明

一応受験ブログでもあるので数学的帰納法についておさらいしておきましょう。
数学的帰納法は何かの数学的なルールや決まりを証明するときに用いられる証明方法です。
例題)nが自然数のとき、2^n(2のn乗)>nを証明せよ。
n=1の時 2>1より成立
n=kの時、成立すると仮定すると
2^k>k・・・①
両辺を2倍して、
2^(k+1)>2✖︎k(>k+1)
となり、k+1の時にも成り立つ。
よって、2^n(2のn乗)>n
のように、証明できます!
ここから二浪が現役であるかを確かめていきます。
(Ⅰ)とある人間がn=1のとき、すなわち、現役で全落ちするか、合格を放棄し、大学を再受験する場合
こいつは1浪目である。
(Ⅱ)n=2(二浪)の時、現役であると仮定すると、
n=3の時、1浪目である。
n=4の時、2浪目である。
二浪は現役である、よって現役である。
n=5の時、1浪目である。
・
・
のようになる。
よって、n=kの時、現役か1浪のどちらかになり、2浪は現役なのでn=k+1の時は現役か1浪かのいずれかである。
よって、結果はn=2k-1の時1浪、n=2kの時現役(kは自然数)ということになります。
まとめると
1浪目、3浪目・・・は1浪
現役、2浪目、4浪目・・・は現役
つまり、2浪は現役です!
よく二浪は世間的に大丈夫なのか?みたいな話になりますが、医学部如何にかかわらず、現役なのでセーフです!
『二浪は現役』理論を書いてみて
如何だったでしょうか?
今回はこれだけです。
現在n>=2の方、またもしn>=2になった場合、就活で最終面接まで行ったとき人事部の面接官から

この高校卒業してからの空白の時間はなに?
と言われることもあると思います。そんなときは

二浪は現役なので、その時間はバグです。
と言い、この帰納法の証明を始めましょう。

なんだこいつ!?
面接でこんなことを言いやがるとは、大したやつだぜ。。。。。
となるはずです。
※採用されるとは言ってません
私は何の責任も取りませんのでご了承ください!
帰納法で証明しようと思ったのですが、考えれば考えるほど意味がわからなくなってきました。
私が何を言いたかったのかわかる方はTwitterのDMまで来てください・・・
YOROZUブログでは他にもたくさんの記事を書いています!
おすすめ記事
学歴コンプの方におすすめの記事はこちら!!
では、次の記事でお会いしましょう!